¿CÓMO ENCONTRAR LA ECUACIÓN DE UNA RECTA?

DADO :Punto-Pendiente

Un tipo de ecuación lineal es la forma punto-pendiente, la cual nos proporciona la pendiente de una recta y las coordenadas de un punto en ella. La forma punto-pendiente de una ecuación lineal se escribe como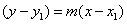.  En ésta ecuación, m es la pendiente y (x₁, y₁) son las coordenadas del punto.

Veamos de dónde es que viene ésta fórmula de punto-pendiente. Aquí está la gráfica de una recta genérica con dos puntos trazados en ella.

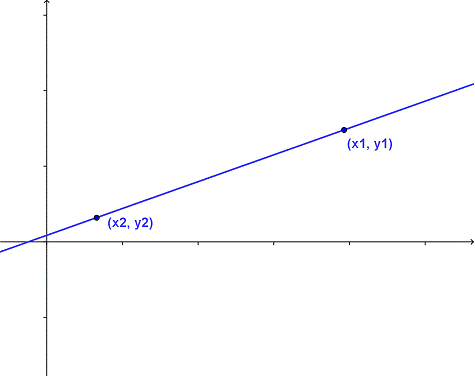
La pendiente de la recta "aumenta conforme va". Ése es el cambio vertical entre dos puntos (la diferencia entre las coordenadas en y) dividida entre el cambio horizontal sobre el mismo segmento (la diferencia entre las corneadas en x). Esto puede escribirse como 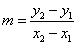. Ésta ecuación es la fórmula de la pendiente.

Ahora digamos que uno de esos puntos es un punto genérico (x, y), lo cual significa que puede ser cualquier punto en la recta, y el otro punto es un punto específico, 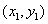. Si sustituimos éstas coordenadas en la fórmula, obtenemos 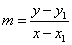. Ahora podemos manipular un poco la ecuación al multiplicar ambos lados de la fórmula por 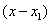. Que se simplifica a 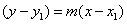_{y operando algebraicamente obtenemos la fórmula y= m x+ b   donde b es la ordenada al origen encontrada algebraicamente.}

_Ejemplo:  Considera la recta que pasa por el punto (1, 3) y tiene una pendiente de .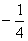

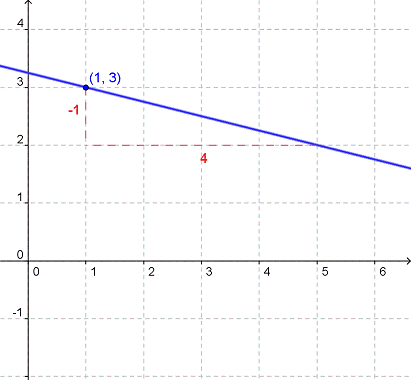
Sustituyendo éstos valores en la fórmula punto-pendiente, obtenemos 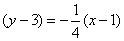 _{y la ecuación luego de operar algebraicamente nos queda y=-1/4 x + 13/4}

DADO: Punto- Punto

Sean P(x₁,y₁) y Q(x₂,y₂) dos puntos de una recta. En base a estos dos puntos conocidos de una recta, es posible determinar su ecuación.
Para ello tomemos un tercer punto R(x,y), también pertenciente a la recta.
Como P, Q y R pertenecen a la misma recta, se tiene que PQ y PR deben tener la misma pendiente. O sea

    y    

Luego, la ecuación de la recta que pasa por dos puntos es:

que también se puede expresar como

Ejemplo:
Determina la ecuación de la recta que pasa por los puntos P(1,2) y Q(3,4)

y - 2 = x - 1

y = x+1

Aquí les dejo un vídeo explicativo: